窥见物理学家大脑中的“精灵” 什么是任意子？

光晶格中的原子自旋纠缠态示意图

　　中国科学技术大学潘建伟等人在国际上首次通过量子调控的方法，在超冷原子体系中发现了拓扑量子物态中的准粒子——任意子，并实现了任意子之间的编织交换过程。

　　日前，中国科学技术大学潘建伟教授及其同事苑震生、陈宇翱等人在国际上首次通过量子调控的方法，在超冷原子体系中发现了拓扑量子物态中的准粒子——任意子，并证实了任意子的分数统计特性，向着实现拓扑量子计算迈出了重要一步。国际权威学术期刊《自然·物理学》发表了该成果。

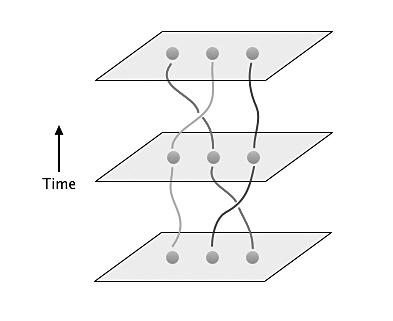
任意子编织的示意图

　　究竟什么是任意子？为什么它会在自然界中出现？

　　自然界存在着奇异粒子

　　1983年，人们在研究当时引人注目的一个宏观量子现象——分数量子霍耳效应时，逐渐意识到这个效应中可能就存在任意子。

　　爱因斯坦曾说过：“常识只是人们在18岁以前对自然形成的一种偏见。”这话很诙谐，但寓意深刻。新的物理现象的发现，就会产生一种全新的理论。新理论相对于旧理论而言，一般总是要违背某些所谓的常识，分数统计及服从分数统计的任意子理论的诞生及其发展过程，就是一个典型的例证。

　　“量子力学中最美妙、最惊人的成就之一，就是给经典力学中毫无意义的全同粒子不可区分性原理赋予了全新的含义，真正不可区分的全同粒子之间具有强烈的相互作用”，中国科技大学陈宇翱教授告诉科技日报记者，这种相互作用通常是通过量子统计规则来实现的。一般说来，全同粒子可分为两类：一类是费米子，具有强烈的排斥作用；另一类是玻色子， 都可以凝聚到能量最低态。

　　“多年来，人们一直认为自然界中只存在费米和玻色两种量子统计。但有人对此提出了疑义，认为可能存在介于玻色子和费米子之间的新的全同粒子，这种粒子一般被称为‘任意子’，它所遵循的统计规则叫分数统计”，陈宇翱说，最早指出这种新的量子统计可能存在的，是两位挪威物理学家。在系统地研究了空间拓扑性质和全同粒子不可区分性原理后，意识到在二维空间中可能存在新的量子统计，1982年美国物理学家F·魏尔茨克提出了任意子的概念。

　　随后研究表明，任意子可以存在于某些理论模型之中，当时的任意子仅仅是寄生在少数几个理论物理学家大脑中的精灵，甚至被认为这只是一些数学上的奇异现象，谁都没有料想到，现实世界中居然还真的会发现这种奇异粒子存在的迹象。1983年，人们在研究当时引人注目的一个宏观量子现象——分数量子霍耳效应时，逐渐意识到这个效应中可能就存在任意子。

　　这在物理学界引起了广泛注意，从而为任意子的理论研究注入了生机。在分数量子霍耳效应理论方面作出了杰出贡献的美国物理学家R.B。劳克林指出，处在费米和玻色子之间的服从1/2统计的任意子的基态可能是超导的，他的理论简单新颖，激发了人们对任意子理论进行深入细致的研究，成为理论物理研究中的一个热点。

　　“当任意子的概念提出时，它似乎违反了量子力学的基本常识，但通过分析量子力学中拓扑性质后，找到了这种粒子在二维空间存在的可能性。”陈宇翱说。

　　任意子只会在二维空间出现

　　二维空间的拓扑性质与现实生活中的螺旋结构有些类似。在二维空间中，两个全同粒子交换位置，总可以分为逆时针和顺时针两个方向的绕动。这就是二维空间中为什么会出现任意子的原因。

　　既然任意子只会在二维空间出现，而我们生活的世界是三维的，那么现实世界中不就没有任意子存在了吗？

　　为了解答记者提出的问题，陈宇翱教授举了个日常生活中的例子：“例如女孩子编辫子，将一部分头发分成三股，依次由外朝里编，每编一次就会形成一个结，连续编两次，头发并不会回到原来的状态，多编几次就编成了一个辫子。又如，我们绕螺旋楼梯登高塔，每走一圈就上升一层，并不是回到原地，但从塔顶往下看，我们只是绕塔在原地兜圈子。”

　　“二维空间的拓扑性质多少与这些具有螺旋结构的例子有些类似”，陈宇翱告诉记者，在二维空间中，两个全同粒子交换位置，总可以分为逆时针和顺时针两个方向的绕动。而在三维空间中脱离一个特定的平面后，或者说一个有特定方向的轴线后，就不再有绕动这样的概念。“所以，在二维空间中两个粒子朝一个方向连续交换两次，波函数并不一定要求回到原来的状态，而完全可以多出一个复相因子，这时波函数的几率分布并不改变”，“不太严格地说，这就是二维空间中为什么会出现任意子的原因”。

　　近几十年来，物理学家对具有低维结构的物质进行了大量的研究发现，这些固体中有许多现象和低维空间的许多性质相关，如固体中的层状结构就具有二维空间的许多性质，这为任意子的存在提供了基础。当1983年美国物理学家霍尔珀林指出，现实世界中已经发现任意子存在的论据时，连任意子理论创导者之一的F·魏尔茨克都表示惊讶不已，大有“叶公好龙”之嫌。

　　“虽然现实世界是三维的，但是固体物质的丰富结构为我们寻找新的复合粒子提供了有利场所，脱离这些物质我们是不可能发现新的任意子的。”陈宇翱说。

　　“窥见”任意子

　　潘建伟研究团队创造性地搭建了新的实验系统并开发了独特的量子调控技术，通过微波反转原子自旋的方法，实现了任意子之间的编织交换过程。

　　任意子的理论被提出后不久，物理学家就在实验中捕捉到了它的踪迹。但如何直接实验观测任意子交换时产生的拓扑相位，进而验证其分数统计特性，一直是一个巨大的实验挑战。

　　10多年前，潘建伟研究团队就开始了对拓扑量子计算的研究并取得了一系列成果。近期，他们创造性地搭建了新的实验系统并开发了独特的量子调控技术，研发了自旋依赖的超晶格系统来囚禁和操控超冷原子，成功操控光晶格中约800个超冷原子同时产生了约200个四原子自旋纠缠态。他们首次观测到了四体环交换相互作用，并通过微波反转原子自旋的方法，实现了任意子之间的编织交换过程，首次在光晶格体系中直接观测到了任意子交换产生的分数拓扑相位。

　　“研究成果的实现，的确是一件令人激动的成就。”陈宇翱表示，这将为进一步研究任意子的拓扑性质提供新的实验平台和手段，将推动拓扑量子计算和晶格规范场量子模拟领域的研究进展。

　　有学者甚至提出一个大胆的设想，利用拓扑材料保护量子比特并操控材料中的任意子进行量子计算。而理论研究表明，拓扑量子计算可以达到很高的容错能力，进而激发了科学家们研制量子计算机的热情。

　　“现在我们已经发现自然界中确实存在任意子，这极大地丰富了量子理论，使我们对物质世界有了更深刻的认识。可以相信，随着人们对具有层状结构的物质进行深入的研究，任意子理论会具有更广泛的应用前景，但其中还有许多基本问题有待去研究、去探索。”陈宇翱说。